Nous avons toujours nourri un vif intérêt pour l’approche comportementale de l’investissement. Sa richesse tient à l’originalité et à la créativité qu’elle mobilise : sonder nos biais, nos intuitions, nos automatismes — bref, ces forces invisibles qui guident nos décisions plus souvent qu’on ne l’admet.
Mais ne nous y trompons pas : cette approche, si féconde soit-elle, a ses limites. Comme le rappelait Richard Feynman : « La réalité doit primer […] car la nature ne peut être trompée. »
La vraie question devient alors : qu’appelle-t-on “réalité” en finance ? Les causes (humaines) ou les conséquences (mesurables) ?
En économie, la réalité prend souvent la forme de données : séries chiffrées, modèles, équations. Elles aident à comprendre ce qu’ont traversé des entreprises, des États, voire des civilisations. Elle contribue aussi, parfois, à reconnaître des signaux déjà vus par le passé, et à en tirer les bonnes leçons, au bon moment.
Encore faut-il être suffisamment lucide – ou averti – pour savoir quelles sont les données les plus constituantes de cette fameuse réalité.
Prenons l’exemple de la Rome antique.
Un empire florissant, puits culturel pour l’Europe, l’Asie mineure et l’Afrique du Nord, berceau d’innovations scientifiques, techniques et philosophiques encore vivantes deux millénaires plus tard. Mais aujourd’hui encore, les causes de sa chute demeurent l’objet de débats passionnés, bien que la réalité de sa disparition n’ait échappé à personne.
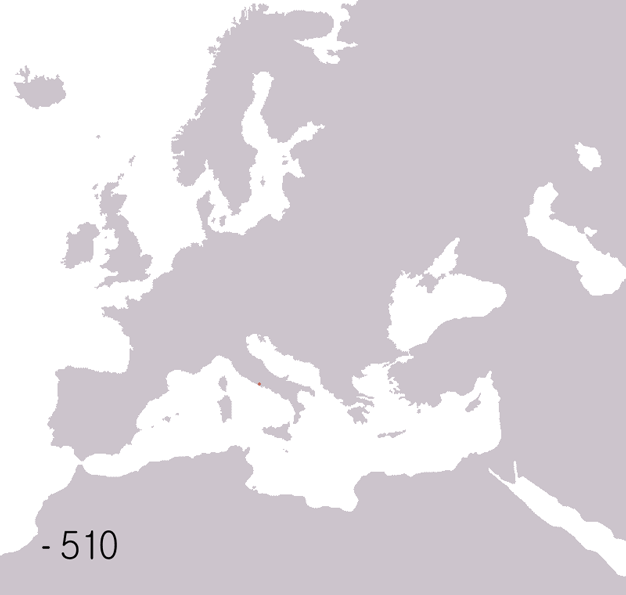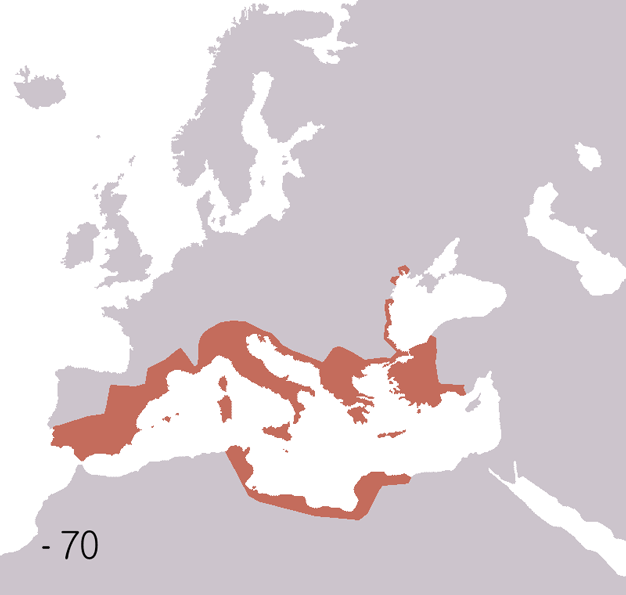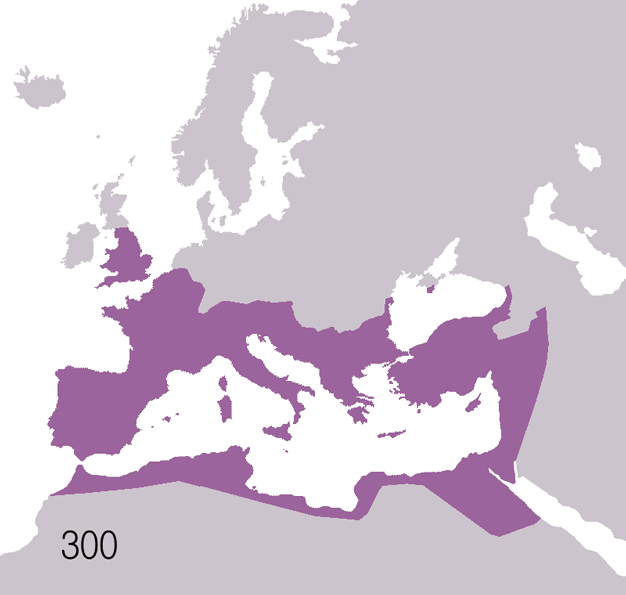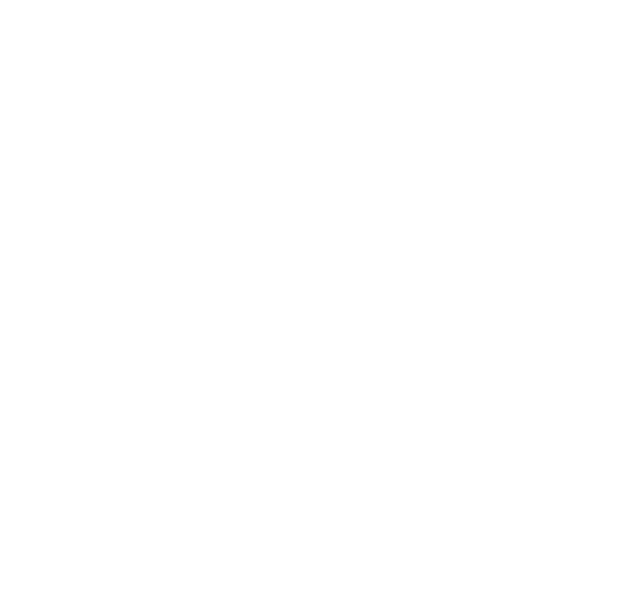
Difficultés administratives : gouverner un empire aussi vaste sans outils modernes relevait de la gageure.
Problèmes sociaux internes : appauvrissement de la classe paysanne, nourricière de l’empire pour une large partie.
Érosion culturelle : le socle romain s’est dilué dans la diversité des peuples intégrés.
Coût militaire : une expansion quasi perpétuelle exigeait des sacrifices humains et financiers colossaux.
Pour bien restituer la toute puissance de ce vaste empire, rappelons qu’au IIᵉ siècle apr. J.-C., à son apogée, Rome comptait environ 400 000 soldats, nécessitant près de 16 000 recrues annuelles pour entretenir cet effectif.
Un siècle plus tard, alors que s’amorçait son déclin, l’armée dépassait les 600 000 hommes, avec des pics de recrutement supérieurs à 23 000 par an. Un rythme, vous en conviendrez, difficilement soutenable. Car le nerf de la guerre reste le financement. L’armée, quoique publique dans ses modalités constituantes, n’échappe pas au besoin impérieux de fonds.
En dépit de ses succès trans-méditerranéens, Rome dut recourir massivement à la dévaluation monétaire pour alimenter sa machine expansionniste.
Cette dévaluation monétaire ne fut, bien sûr, pas sans conséquence.
Le denier (pièce de monnaie constituée d’argent), frappé pour la première fois en 211 av. J.-C., tout comme l’aureus (monnaie en or) perdirent progressivement de leur valeur.
Sous Néron (54–68 apr. J.-C.), la teneur en argent pur du denier fut réduite pour la première fois. On abaisse poids et titre : le fin passe d’environ 97–98 % à ~93–95 % d’argent, première étape d’une trajectoire descendante.
Sous Caracalla (211–217 apr. J.-C.) le denier ne fut plus émis qu’avec une teneur maximale de 50% d’argent.
Sous Gallien (260-270 apr. J.-C.) le denier devint un ersatz, parfois composé de moins de 5 % d’argent.
L’historien Michael Crawford, dans son ouvrage History of the Roman Republican Coinage, soulignera que l’inflation sapait la confiance des soldats comme des citoyens dans la valeur même de l’État.
Rome avait financé son présent au prix de son avenir avec une mécanique simple : l’expansion perpétuelle.
L’accroissement de l’Empire reposait sur une mécanique simple : se financer grâce aux conquêtes. Chaque campagne coûtait cher en hommes et en argent, mais devait être compensée par le butin, les indemnités et les esclaves des vaincus. Ces conquêtes fournissaient non seulement de l’or et des terres, mais entraînaient en outre l’ingestion de populations et de cultures nouvelles qu’il fallait intégrer. Dans le même temps, l’Empire voyait sa paysannerie s’appauvrir, concurrencée par les grandes exploitations esclavagistes.
Pour maintenir la plèbe docile et l’adhésion des élites, Rome misait inlassablement sur la prochaine guerre, censée générer un nouveau flux de richesses. Ce modèle d’expansion et redistribution permanente ne tenait que sous deux conditions : que les armées demeurent victorieuses, et que l’État trouve à financer son effort de guerre constant, notamment en dévaluant le denier.
Une architecture ambitieuse, mais d’une fragilité extrême. Et comme le résumait l’historien Arnold Toynbee : « Les civilisations ne meurent pas assassinées, elles se suicident. »
Présentée ainsi, on pourrait croire que la dévaluation monétaire, à elle seule, fut l’acte de décès du Caput Mundi. Mais l’histoire n’est jamais si simple, ni si commode. La chute de Rome ne s’est pas écrite en une seule ligne, mais en une polyphonie de désordres.
Aux frappes de deniers de plus en plus dénués d’argent et de valeur s’ajoutèrent des famines tenaces, quand l’Empire n’arrivait plus à nourrir ses villes comme jadis ; l’accès à l’eau, ressource vitale, devint inégal, parfois défaillant dans des régions entières. Les champs, usés et mal exploités, fournirent moins, les greniers se vidèrent.
L’administration, autrefois modèle d’efficacité, se dilua dans l’immensité d’un territoire trop vaste pour rester cohérent ; les querelles de palais et les guerres civiles épuisèrent l’autorité centrale. Et aux confins, là où Rome prétendait rayonner, les provinces s’émancipèrent, ou bien ployèrent sous les assauts germaniques et perses.
Ainsi, plus qu’un coup de poignard unique, la fin de Rome fut une hémorragie diffuse, où chaque plaie — économique, sociale, politique, militaire — saigna un peu plus l’Empire.
Alors posons la question autrement : si une bourse romaine avait existé, quel pari aurait-il fallu faire ? Quel signal, parmi cette mosaïque de désordres, aurait mérité d’inspirer le short du siècle ? Et surtout, quelle gravité accorder à chacun de ces facteurs, dont chacun, isolément, aurait pu suffire à faire chavirer le navire impérial ?
Le monde économico-financier : un problème humain ou un problème de maths ?
Et c’est là que surgit la vraie difficulté : comment pondérer ces facteurs ? Faut-il les hiérarchiser, les ordonner, les classer dans quelque tableau savant ? Faut-il, au contraire, se réfugier dans une vision holistique — « les causes sont toujours multiples » — qui a le mérite d’être irréfutable… mais demeure impossible à modéliser ?
Ou bien faut-il, plus radicalement, les balayer d’un revers de main, et assumer de bâtir son calcul économico-financier en les ignorant sciemment
Reprenons dans l’ordre.
A ceux qui pensent que chaque fait a son propre poids, Friedrich A. von Hayek (1899–1992), figure de l’école autrichienne, rappelait que « l’économie n’est pas une science des quantités, mais une science de l’action humaine. ». Aussi, chaque fait pèse dans la balance, et les ramifications de ces faits peuvent être innombrables.
Reconnaître cette force indomptable est une chose, savoir comment la hiérarchiser en est une autre. Cependant, des modèles existent. L’analyse micro ou l’analyse macro sont déjà, à leur niveau, des approximations des comportements humains et de leurs conséquences à certaines échelles.
Et ça fonctionne. Mais c’est insuffisant pour certains investisseurs.
Cherchons donc encore.
À rebours du postulat de Hayek, d’autres chercheurs considèrent que les crises ne sont pas d’origine humaine. Ainsi pour Eugene Fama, père de la théorie des marchés efficients, toute l’information disponible est déjà contenue dans les prix. Fama défend d’une certaine manière une vision holistique du monde et des marchés, où les agents économiques, la nature humaine et les impondérables de la vie sont en temps réels communiqués aux uns et aux autres par l’intermédiaire des prix. Les crises ne seraient alors que la matérialisation de données inscrites dans la structure des marchés, bien avant leur révélation spectaculaire.
Cela reviendrait, grossièrement, à dire que l’économie craque… parce qu’elle doit craquer.
C’est alors que le génie de Benoît Mandelbrot (1924–2010), mathématicien polono-franco-américain, pionnier des fractales, apporte une perspective singulière : « Les marchés peuvent sembler chaotiques, mais ils obéissent à des règles que nous commençons seulement à comprendre. »
Des règles qui échappent à des logiques comportementales, mais qui sont en revanche parfaitement modélisables.
Les fractales sont des structures dont les motifs se répètent à toutes les échelles. On parle d’auto-similarité. Mandelbrot a montré que cette logique s’applique également aux marchés financiers : un graphique journalier ressemble à un graphique mensuel, qui lui-même ressemble à un graphique décennal, et ainsi de suite. À chaque échelle, les cycles de hausse et de baisse semblent se répliquer. C’est une expérience fractale que chaque investisseur à déjà pu vivre.
Mais la vision de Mandelbrot est bien plus élégante que cela.
La volatilité n’est pas aléatoire
L’intuition de Mandelbrot est la suivante : les marchés conservent la mémoire de leurs secousses.
L’une des grandes révolutions intellectuelles en finance a été de comprendre que la volatilité ne se comporte pas comme un bruit blanc désordonné. Elle n’est pas dispersée au hasard : elle se regroupe en grappes (on parle de volatility clustering). Autrement dit, les marchés connaissent de longs épisodes de calme, suivis de longs épisodes de tempête. La turbulence appelle la turbulence, et la stabilité se prolonge jusqu’à ce qu’une cassure structurelle vienne rompre l’équilibre.
En langage statistique, cela s’appelle une autocorrélation de la volatilité. Les rendements eux-mêmes — c’est-à-dire les variations de prix d’un jour à l’autre — ne montrent pratiquement aucune corrélation exploitable : le passé ne prédit pas le futur.
Mais si l’on regarde non pas les rendements, mais leurs proxys (un indicateur empirique basé sur une donnée), comme les rendements au carré ou leurs valeurs absolues, la dépendance saute aux yeux. Les chocs de grande ampleur tendent à s’enchaîner, même sans nouvelle fondamentale. Cette idée a été confirmée empiriquement au fil des décennies et fait désormais partie des “stylized facts” de la finance : des régularités observées systématiquement sur les séries financières, quel que soit l’actif ou la période. Ainsi, les crises financières ne seraient pas forcément des « accidents » extérieurs, mais plutôt des révélateurs soudains d’une structure sous-jacente instable, latente, que le marché portait déjà en lui.
La réalité s’observe donc à une échelle presque irréductible : celle des mathématiques.
Inutile d’attendre un COVID-26 ou un nouveau lundi noir pour profiter (ou s’inquiéter) d’un pic de volatilité.
D’après Mandealbrot, on peut l’estimer à partir des pics de volatilité précédents (donc sans se soucier des événements) car les marchés gardent mémoire de la volatilité.
Entre 1990 et 2016, les rendements journaliers du S&P 500 ont été analysés avec un modèle GARCH(1,1), l’outil de référence pour étudier la dynamique de la variance conditionnelle, c’est à dire l’évolution dans le temps de la volatilité attendue d’un actif, calculée en fonction de l’information disponible sur les chocs et la volatilité passés.
Résultat :
α ≈ 0,075 (mesure l’impact immédiat des chocs)
β ≈ 0,915 (persistance de la volatilité, soit la mémoire de longue durée de la volatilité passée)
donc α + β ≈ 0,99
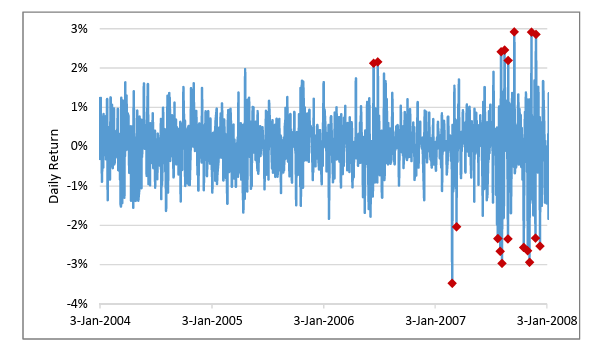
Un chiffre proche de 1 signifie une mémoire longue : un choc de volatilité laisse une empreinte durable. Une journée où l’indice perd plus de 2 % n’est pas un simple accident isolé : c’est un signal que le régime de volatilité a basculé, et que les turbulences risquent de se prolonger pendant des jours, voire des semaines.
Ce type de résultat a été documenté des dizaines de fois, sur le S&P 500 comme sur d’autres indices, les marchés de change ou les matières premières. La signature est universelle : la volatilité s’accroche, elle se nourrit d’elle-même.
Ce comportement est similaire à celui d’un élastique : une faible tension générera peut d’amplitude, donc pas ou peu de rebond. Mais une tension extrême générera de nombreux rebonds, et les premiers seront d’amplitudes significatives.